单选题
- A、
- B、
- C、
- D、
互不重合的A,B,C三点在同一直线上,已知AC=2a+1,BC=a+4,AB=3a,这三点的位置关系是( )
- A、 点A在B,C两点之间
- B、 点B在A,C两点之间
- C、 点C在A,B两点之间
- D、 无法确定
下列因式分解正确的是( )
- A、 x2+9=(x+3)(x﹣3)
- B、 x2+x﹣6=(x﹣2)(x+3)
- C、 3x﹣6y+3=3(x﹣2y)
- D、 x2+2x﹣1=(x﹣1)2
已知  中不含
中不含  的二次项,则
的二次项,则  的值是( )
的值是( )
- A、 3
- B、 2
- C、 -3
- D、 -2
如果单项式  和
和  是同类项,则m和n的值是( )
是同类项,则m和n的值是( )
- A、 2,1
- B、 -2,1
- C、 -1,2
- D、
,
设  ,则
,则  的值为( )
的值为( )
- A、
- B、
- C、 1
- D、
下列计算中错误的是( )
- A、 4a5b3c2÷(﹣2a2bc)2=ab
- B、 (a+1)(a﹣1)(a2+1)=a4﹣1
- C、 4x2y•(﹣
y)÷4x2y2=﹣
- D、 25×(
x2﹣
x+1)=x2﹣
x+1
若代数式 的值与x的取值无关,则
的值与x的取值无关,则 的值为( )
的值为( )
- A、 6
- B、 -6
- C、 2
- D、 -2
若  与
与  的积为
的积为  ,则
,则  为( )
为( )
- A、
- B、
- C、
- D、
已知  ,其中☆代表一个常数,则☆的值为( )
,其中☆代表一个常数,则☆的值为( )
- A、 1
- B、 2
- C、 3
- D、 4
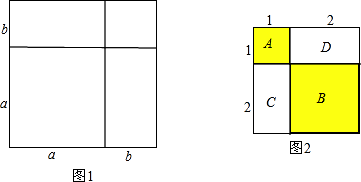
把五张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个大长方形(长为m,宽为n内(如图②),大长方形未被卡片覆盖的部分用阴影表示.当m不变,n变长时,阴影部分的面积差总保持不变,则a,b应满足的关系为( )
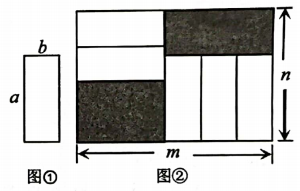
- A、 a=5b
- B、 a=3b
- C、 a=2b
- D、
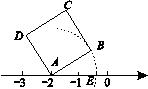
如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:
①abc<0;②a(b+c)>0;③a﹣c=b;④ .
![]()
其中正确的个数有 ( )
- A、 1个
- B、 2个
- C、 3个
- D、 4个
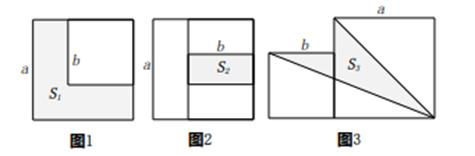
有两个正方形A,B.现将B放在A的内部得图甲,将A,B构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12,若三个正方形A和两个正方形B得图丙,则阴影部分的面积为( )
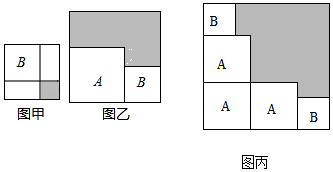
- A、 28
- B、 29
- C、 30
- D、 31
- A、 8
- B、 6
- C、 2
- D、 0
已知  ,则
,则  的值为( )
的值为( )
- A、 4
- B、 2
- C、 -2
- D、 -4