单选题
下列各数中,绝对值最小的数是( )
- A、 0
- B、 -1
- C、 -5
- D、 2
下列运算正确的是( )
- A、
- B、
- C、
- D、
由圆柱和长方体(底面为正方形)组成的几何体如图放置,该几何体的俯视图是( )
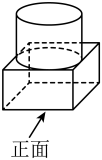
- A、

- B、

- C、

- D、

中国人很早就开始使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放着表示正数,斜放着表示负数,如图(1)表示 . 按照这种表示法,如图(2)表示的是( )
. 按照这种表示法,如图(2)表示的是( )

- A、
- B、
- C、
- D、
圆的周长公式是人类文明进程中最伟大的公式之一.现在计算圆周率的精确度主要用于检验计算机的运算速度,目前人类能够计算到圆周率的628万亿位.把数据“62.8万亿”用科学记数法表示为( )
- A、
- B、
- C、
- D、
如图,用若干个全等的正五边形排成圆环状,图中所示的是其中3个正五边形的位置.若完成这一圆环排列,共需要正五边形的个数是( )

- A、 7个
- B、 8个
- C、 9个
- D、 10个
化简 的结果是( )
的结果是( )
- A、 2
- B、
- C、
- D、









