备考2024年浙江中考数学一轮复习专题22.2圆真题模拟集训

日期: 2025-03-21 一轮复习来源：出卷网

选择题（每题2分，共24分）

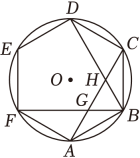
如图，点A ， B ， C在⊙O上，连结AB ， AC ， OB ， OC ．若∠BAC＝50°，则∠BOC的度数是（　　）

A、 80°

B、 90°

C、 100°

D、 110°

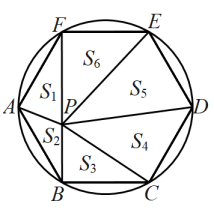
如图，已知△ABC内接于半径为1的⊙O，∠BAC=θ（θ是锐角），则△ABC的面积的最大值为（）

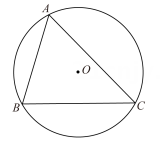
A、 cosθ(1+cosθ)

B、 cosθ(1+sinθ)

C、 sinθ(1+sinθ)

D、 sinθ(1+cosθ)

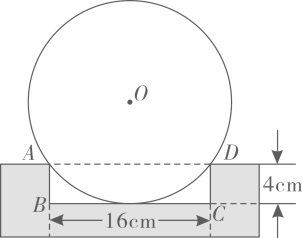
某仿古墙上原有一个矩形的门洞，现要将它改为一个圆弧形的门洞，圆弧所在的圆外接于矩形，如图.已知矩形的宽为2m，高为2 $\text{[math]}$ m，则改建后门洞的圆弧长是（）

A、 $\text{[math]}$ m

B、 $\text{[math]}$ m

C、 $\text{[math]}$ m

D、（ $\text{[math]}$ +2）m

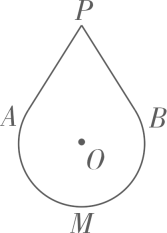
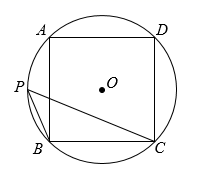
如图，正方形ABCD内接于 $\text{[math]}$ ，点P在 $\text{[math]}$ 上，则 $\text{[math]}$ 的度数为（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，以该三角形的三条边为边向形外作正方形，正方形的顶点 $\text{[math]}$ 都在同一个圆上.记该圆面积为 $\text{[math]}$ ， $\text{[math]}$ 面积为 $\text{[math]}$ ，则 $\text{[math]}$ 的值是（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

已知平面内有⊙O和点A，B，若⊙O半径为2cm，线段OA＝3cm，OB＝2cm，则直线AB与⊙O的位置关系为（）

A、相离

B、相交

C、相切

D、相交或相切

已知 $\text{[math]}$ 的直径 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的弦， $\text{[math]}$ ，垂足为 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$ 或 $\text{[math]}$

D、 $\text{[math]}$ 或 $\text{[math]}$

如图，在圆内接正六边形ABCDEF中，BF ， BD分别交AC于点G ， H ，若该圆的半径为12，则线段GH的长为（）

A、 6

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 8

如图，点O为△ABC的内心，∠B＝60°，点M，N分别为AB，且OM＝ON．甲、乙两人有如下判断：甲：∠MON＝120°：乙：当MN⊥BC时，△MON的周长有最小值．则下列说法正确的是（）

A、只有甲正确

B、只有乙正确

C、甲、乙都正确

D、甲、乙都错误

如图，在Rt△ABC中，∠C=90°，BC=4， $\text{[math]}$ ． ⊙C的半径长为2，P是△ABC边上一动点（可以与顶点重合），并且点P到⊙C的切线长为m．若满足条件的点P有4个，则m的取值范围是（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

如图，正六边形 $\text{[math]}$ ， P点在 $\text{[math]}$ 上，记图中的面积为 $\text{[math]}$ ，已知正六边形边长，下列式子中不能确定的式子的是（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

如图是某款“不倒翁”的示意图， $\text{[math]}$ ， $\text{[math]}$ 分别与 $\text{[math]}$ 所在圆相切于点 $\text{[math]}$ ， $\text{[math]}$ ．若该圆半径是 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长是（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

填空题（每题3分，共21分）

若扇形的圆心角为 $\text{[math]}$ ，半径为18，则它的弧长为。

如图是一个圆形餐盘的正面及其固定支架的截面图，凹槽ABCD是矩形.当䝳盘正立且紧靠支架于点A，D时，恰好与BC边相切，则此餐盘的半径等于 $\text{[math]}$ .

如图，圆锥形烟囱帽的底面半径为 $\text{[math]}$ ，母线长为 $\text{[math]}$ ，则烟囱帽的侧面积为 $\text{[math]}$ ．（结果保留 $\text{[math]}$ ）

如图所示，半径为1的圆心角为60°的扇形纸片OAB在直线L上向右做无滑动的滚动．且滚动至扇形O′A′B′处，则顶点O所经过的路线总长是

如图，PA ， PB分别与半径为3的⊙O相切于点A ， B ，直线CD分别交PA ， PB于点C ， D ，并切⊙O于点E ，当PO＝6时，△PCD的周长为．

如图，在菱形 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 上的点， $\text{[math]}$ ，连接 $\text{[math]}$ ，与过 $\text{[math]}$ 三点的 $\text{[math]}$ 相切于 $\text{[math]}$ 点，已知 $\text{[math]}$ ，则 $\text{[math]}$ °．

图1是 $\text{[math]}$ 方格绘成的七巧板图案，每个小方格的边长为 $\text{[math]}$ ，现将它前拼成一个“房子”造型（如图2），过左侧的三个端点作圆，并在圆内右侧部分留出矩形CDEF作为题字区域（点A，E，D，B在圆上，点C，F在AB上），形成一幅装饰画，则圆的半径为.若点A，N，M在同一直线上， $\text{[math]}$ ，则题字区域的面积为.

作图题（共6分）

请仅用无刻度的直尺完成下列画图，不写画法，保留画图痕迹．

解答题（共6题，共49分）

如图，⊙O是△ABC的外接圆，AE是⊙O的直径，点B $\text{[math]}$ 的中点，过点B的切线与AC的延长线交于点D.

①求证：BD⊥AD；

②若AC＝9，tan∠ABC＝ $\text{[math]}$ ，求⊙O的半径.

如图，以△ABC的一边AB为直径作⊙O ， ⊙O与BC边的交点D恰好为BC的中点，DE⊥AC ．

如图，在Rt $\text{[math]}$ 中， $\text{[math]}$ 为AC边上一点，连结OB.以OC为半径的半圆与AB边相切于点 $\text{[math]}$ ，交AC边于点 $\text{[math]}$ .

如图，在 $\text{[math]}$ 中，直径 $\text{[math]}$ 垂直弦 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，作 $\text{[math]}$ 于点 $\text{[math]}$ ，交线段 $\text{[math]}$ 于点 $\text{[math]}$ （不与点 $\text{[math]}$ 重合），连接 $\text{[math]}$ ．

我们可以通过中心投影的方法建立圆上的点与直线上点的对应关系，用直线上点的位置刻画圆上点的位置，如图，AB是 $\text{[math]}$ 的直径，直线l是 $\text{[math]}$ 的切线，B为切点．P，Q是圆上两点（不与点A重合，且在直径AB的同侧），分别作射线AP，AQ交直线l于点C，点D．

如图1，在 $\text{[math]}$ 中，直径 $\text{[math]}$ 于点F，点E为 $\text{[math]}$ 上一点，点C为弧 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ，交 $\text{[math]}$ 于点G．

实践探究题（共2题，共20分）

旋转的图形带来结论的奥秘.已知 $\text{[math]}$ ，将 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转得到 $\text{[math]}$ .

初步探索

素材1：

如图①，连接对应点 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ .

素材2：

如图②，以 $\text{[math]}$ 为圆心， $\text{[math]}$ 边上的高 $\text{[math]}$ 为半径作 $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 相切.

问题解决

（1）（ⅰ）请证明素材1所发现的结论.

（ⅱ）如图2，过点 $\text{[math]}$ 作 $\text{[math]}$ ，垂足为 $\text{[math]}$ .证明途径可以用下面的框图表示，请填写其中的空格.

深入研究

（2）在 $\text{[math]}$ 满足 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$ 是 $\text{[math]}$ 的中点， $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转得 $\text{[math]}$ .

（ⅰ）如图③，当边 $\text{[math]}$ 恰好经过点 $\text{[math]}$ 时，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的长为▲.

（ⅱ）若一时边 $\text{[math]}$ 所在直线恰好经过点 $\text{[math]}$ ，于图④中利用无刻度的直尺和圆规作出直线.（只保留作图痕迹）

（3）在（2）的条件下，如图⑤，在旋转过程中，直线 $\text{[math]}$ ， $\text{[math]}$ 交于点 $\text{[math]}$ ，求 $\text{[math]}$ 的最大值为▲.

项目化学习：车轮的形状．

【问题提出】车轮为什么要做成圆形，这里面有什么数学原理?

相关试卷推荐

友情链接

组卷网课件下载备课易 StirlingPdf 排课软件云字帖

2016-2022 组卷题库
组卷题库试题答案查询