二次根式
高空抛物极其危险,是我们必须杜绝的行为.据研究,高空抛物下落的时间 (单位:s)和高度h(单位:m)近似满足公式
(单位:s)和高度h(单位:m)近似满足公式 (不考虑风速的影响).记从
(不考虑风速的影响).记从 高空抛物到落地所需时间为
高空抛物到落地所需时间为 . 从
. 从 高空抛物到落地所需时间为
高空抛物到落地所需时间为 , 则
, 则 的值是( )
的值是( )
- A、
- B、
- C、
- D、 2
一元二次方程
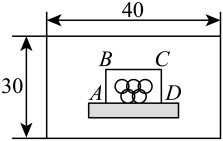
如图,在一块长为  ,宽为
,宽为  的矩形
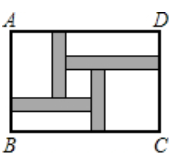
的矩形  空地内修建四条宽度相等,且与矩形各边垂直的道路.四条道路围成的中间部分恰好是一个正方形,且边长是道路宽的4倍,道路占地总面积为
空地内修建四条宽度相等,且与矩形各边垂直的道路.四条道路围成的中间部分恰好是一个正方形,且边长是道路宽的4倍,道路占地总面积为  .设道路宽为
.设道路宽为  ,则以下方程正确的是( )
,则以下方程正确的是( )
- A、
- B、
- C、
- D、
目前我国建立了比较完善的经济困难学生资助体系,某校2021年给贫困学生每人400元补贴,2023年给贫困学生每人560元补贴,设每年发放的资助金额的平均增长率为x,则下面列出的方程中正确的是( )
- A、
- B、
- C、
- D、
某医疗物资制造厂原来每件产品的生产成本是100元,为提高生产效率改进了生产技术,连续两次降低成本后,成本是81元,则平均每次降低成本的百分率为 ( )
- A、 8.5%
- B、 9%
- C、 9.5%
- D、 10%
数据分析初步
某班级采用小组学习制,在一次数学单元测试中,第一组成员的测试成绩分别为:96,90,100,80,96,其中得分80的同学有一道题目被老师误判,其实际得分应该为90分,那么该小组的实际成绩与之前成绩相比,下列说法正确的是( )
- A、 数据的平均数不变
- B、 数据的众数不变
- C、 数据的中位数不变
- D、 数据的方差不变
在一次素养比赛中,6位学生的成绩分别为65分,65分,80分,85分,90分,90分,统计时误将一位学生的成绩65分记成了60分,则其中不受影响的统计量是( )
- A、 平均数
- B、 中位数
- C、 众数
- D、 方差

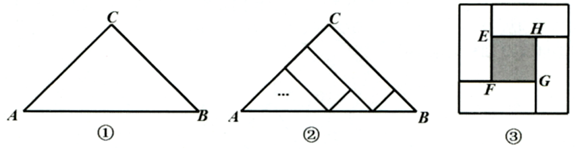



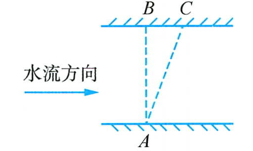



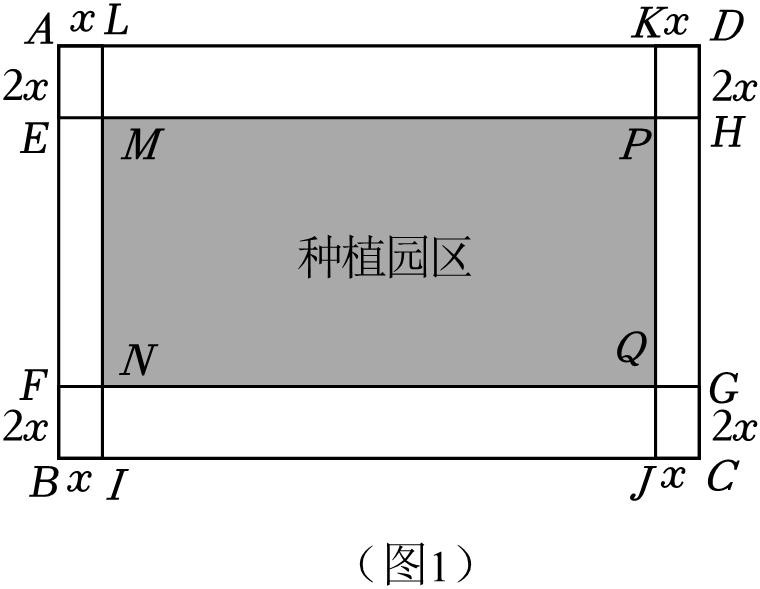






 请完成下列问题:
请完成下列问题: