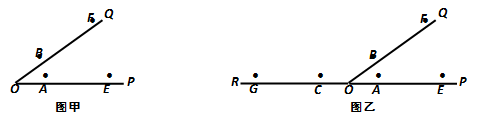选择题
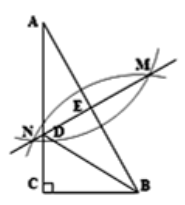
综合实践课上,嘉嘉画出 , 如图1,利用尺规作图作
, 如图1,利用尺规作图作 的角平分线
的角平分线 . 其作图过程如下:
. 其作图过程如下:
如图2,在射线
上取一点D(不与点O重合),作
, 且点C落在
内部;
如图3,以点D为圆心,以
长为半径作弧,交射线
于点P , 作射线
, 射线
就是
的平分线.

图1 图2 图3
在嘉嘉的作法中,判断射线是
的平分线过程中不可能用到的依据是( )
- A、 同位角相等,两直线平行
- B、 两直线平行,内错角相等
- C、 等边对等角
- D、 到角两边距离相等的点在这个角的角平分线上
已知△ABC ,  ,
,  . 用尺规在边AC上求作一点P , 使
. 用尺规在边AC上求作一点P , 使 . 下图是甲、乙两位同学的作图,下列判断正确的是( )
. 下图是甲、乙两位同学的作图,下列判断正确的是( )

- A、 甲、乙的作图均正确
- B、 甲、乙的作图均不正确
- C、 只有甲的作图正确
- D、 只有乙的作图正确
如图,用尺规作出 , 则作图痕迹中,弧
, 则作图痕迹中,弧 是( )
是( )

- A、 以点
为圆心,
为半径的弧
- B、 以点
为圆心,
为半径的弧
- C、 以点
为圆心,
为半径的弧
- D、 以点
为圆心,
为半径的弧
用尺规作图,已知三边作三角形,用到的基本作图是( )
- A、 作一个角等于已知角
- B、 作已知直线的垂线
- C、 作一条线段等于已知线段
- D、 作角的平分线