单选题
二次函数y=(x-3)2+1的最小值是( )
- A、 3
- B、 -3
- C、 1
- D、 -1
已知抛物线 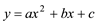 的开口向下,顶点坐标为(2,-3) ,那么该抛物线有( )
的开口向下,顶点坐标为(2,-3) ,那么该抛物线有( )
- A、 最小值 -3
- B、 最大值-3
- C、 最小值2
- D、 最大值2
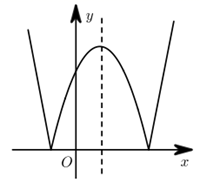
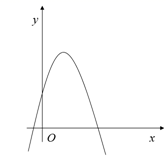
二次函数  (
(  )的图象如图所示,则下列结论:①a<0;②函数有最小值;③ c>0,③
)的图象如图所示,则下列结论:①a<0;②函数有最小值;③ c>0,③  < 0,其中正确的个数是( )
< 0,其中正确的个数是( )
- A、 1个
- B、 2个
- C、 3个
- D、 4个
若抛物线y=(x+1)2+c与y轴相交于点(0,﹣5),则y的最小值为( )
- A、 ﹣6
- B、 6
- C、 ﹣5
- D、 5
二次函数y=ax2+bx+c的自变量x和函数y的部分对应值如表:
| x | … | 0 | | 1 | 2 | 3 | 4 | … |
| y | … | 4 | 5 | 4 | ﹣4 | ﹣20 | ﹣45 | … |
则该二次函数y在所给自变量x(﹣2≤x≤2)的取值范围内的最小值是( )
- A、 ﹣45
- B、 ﹣20
- C、 ﹣4
- D、 0
已知非负数a,b,c满足a+b=3且c﹣3a=﹣6,设y=a2+b+c的最大值为m,最小值为n,则m﹣n的值是( )
- A、 16
- B、 15
- C、 9
- D、 7
已知抛物线y=ax2﹣2ax+3不经过第四象限.当﹣1≤x≤2时,y的最大值与最小值的差是12,则a的值是( )
- A、 ﹣3
- B、 3
- C、 4
- D、 12
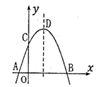
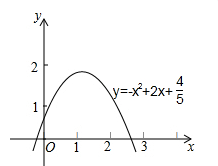
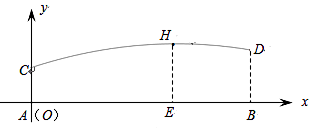
如图,已知二次函数的图象(0≤x≤1+2  ).关于该函数在所给自变量取值范围内,下列说法正确的是( )
).关于该函数在所给自变量取值范围内,下列说法正确的是( )
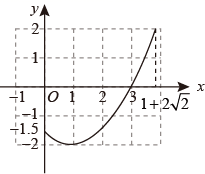
- A、 有最小值﹣2,无最大值
- B、 有最小值﹣2,有最大值﹣1.5
- C、 有最小值﹣2,有最大值2
- D、 有最小值﹣1.5,有最大值2
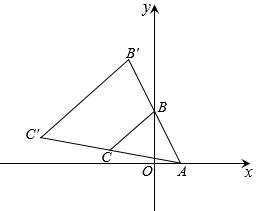
如图,一条抛物线与x轴相交于M,N两点(点M在点N的左侧),其顶点P在线段AB上移动,点A,B的坐标分别为(﹣2,﹣3),(1,﹣3),点N的横坐标的最大值为4,则点M的横坐标的最小值为( )
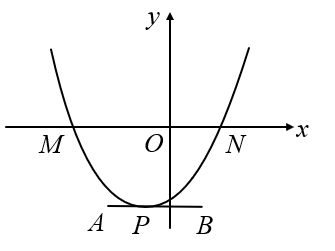
- A、 ﹣1
- B、 ﹣3
- C、 ﹣5
- D、 ﹣7
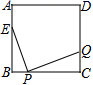
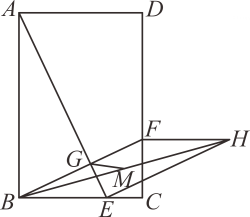
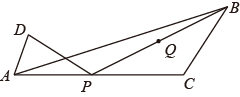
如图,已知AB=8,P为线段AB上一个动点,分别以AP,PB为边在AB的同侧作菱形APCD和PBFE,点P,C,E在一条直线上,∠DAP=60°,M,N分别是对角线AC,BE的中点,当点P在线段AB上移动时,点M,N之间的距离最短为( )
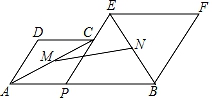
- A、
- B、
- C、 4
- D、 3
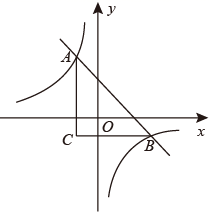
如图,抛物线y1=a(x+1)2﹣5与抛物线y2=﹣a(x﹣1)2+5(a≠0)交于点A(2,4),B(m, ﹣4),若无论x取任何值,y总取y1 ,y2中的最小值,则y的最大值是( )
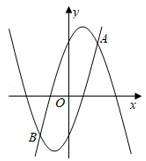
- A、 4
- B、 5
- C、 2
- D、 1
我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式,此公式与古希腊几何学家海伦提出的公式如出一辙,即三角形的三边长分别为a,b,c, 记  ,则其面积
,则其面积  .这个公式也被称为海伦-秦九韶公式.若
.这个公式也被称为海伦-秦九韶公式.若  ,则此三角形面积的最大值为( )
,则此三角形面积的最大值为( )
- A、
- B、 4
- C、
- D、 5
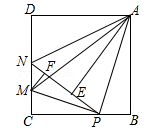
如图,△ABC是一张锐角三角形的纸片,AD是边BC上的高,已知BC=20cm,AD=15cm,从这张纸片上剪一下一个矩形,使矩形的一边在BC上,另两个顶点分别在AB、AC上。则下列结论不正确的是( )

- A、 当△AHG的面积等于矩形面积时,HE的长为5cm
- B、 当HE的长为6cm时,剪下的矩形的边HG是HE的2倍
- C、 当矩形的边HG是HE的2倍时,矩形面积最大
- D、 当矩形的面积最大时,HG的长是10cm
已知:如图,正方形ABCD中,AB=2,AC,BD相交于点O,E,F分别为边BC,CD上的动点(点E,F不与线段BC,CD的端点重合)且BE=CF,连接OE,OF,EF.在点E,F运动的过程中,有下列四个结论:

①△OEF是等腰直角三角形;
②△OEF面积的最小值是 ;
③至少存在一个△ECF,使得△ECF的周长是 ;
④四边形OECF的面积是1.
所有正确结论的序号是( )
- A、 ①②③
- B、 ③④
- C、 ①②④
- D、 ①②③④
新定义:若关于x的一元二次方程:a1(x-m)2+n=0与a2(x-m)2+n=0,称为“同族二次方程”如2(x-3)2+4=0与3(x-3)2+4=0是“同族二次方程”现有关于x的一元二次方程2(x-1)2+1=0与(a+2)x2+(b-4)x+8=0是“同族二次方程”,那么代数式ax2+bx+2018能取的最小值是( )
- A、 2011
- B、 2013
- C、 2018
- D、 2023
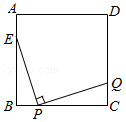
如图,正方形ABCD边长为8,M,N分别是边BC,CD上的两个动点,且AM⊥MN,则AN的最小值是( )
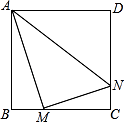
- A、 8
- B、 4
- C、 10
- D、 8