选择题
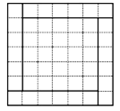
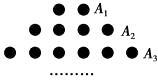
如图,在一个三角点阵中,从上向下数有无数多行,其中各行点数依次为2,4,6,…,2n,…,请你探究出前n行的点数和所满足的规律.若前n行点数和为930,则n=( )
- A、 29
- B、 30
- C、 31
- D、 32
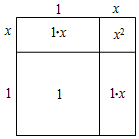
小明和小林在探索代数式x2+ (x≠0)有没有最大(小)值时,小明做了如下探索:
(x≠0)有没有最大(小)值时,小明做了如下探索:
∵x2++2-2 =(x+
)2-2≥-2,
∴小明的结论是x2+的最小值为-2
小林做了如下探索
∵x2+-2+2 =(x-
)2+2≥2,
小林的结论是x2+的最小值为2;则( )
- A、 小明正确
- B、 小林正确
- C、 小明和小林都正确
- D、 小明和小林都不正确
探讨关于x的一元二次方程 总有实数根的条件,下面三名同学给出建议:甲:a,b同号;乙:
总有实数根的条件,下面三名同学给出建议:甲:a,b同号;乙: ;丙:
;丙: . 其中符合条件的是( )
. 其中符合条件的是( )
- A、 甲,乙,丙都正确
- B、 只有甲错误
- C、 甲,乙,丙都错误
- D、 只有乙正确
小宁在研究关于x的一元二次方程x2-4x+m=0时,得到以下4个结论:
①若m=4,则方程有两个相等的实数根;②若m<0,则方程必有两个异号的实数根;③若m<4,则方程的两个实数根不可能都大于2;④若m<-5,则方程的两个实数根一个小于5,另一个大于5.其中结论正确的个数有( )
- A、 1个
- B、 2个
- C、 3个
- D、 4个
已知实数  ,现有甲、乙、丙、丁四人对关于
,现有甲、乙、丙、丁四人对关于  的方程
的方程  进行了讨论:
进行了讨论:
甲说:这一定是关于 的一元二次方程;
乙说:这有可能是关于 的一元一次方程;
丙说:当 时,该方程有实数根;
丁说:只有当 且
时,该方程有实数根.( )
- A、 甲和丙说的对
- B、 甲和丁说的对
- C、 乙和丙说的对
- D、 乙和丁说的对