新考法-探索图形中的数量关系
新考法-结合数学文化
文艺复兴时期,意大利艺术大师达·芬奇曾研究过圆弧所围成的许多图形的面积问题.如图称为达·芬奇的“猫眼”,可看成圆与正方形的各边均相切,切点分别为A,B,C,D,劣弧BD所在圆的圆心为点A或点C.若正方形的边长为2,则图中阴影部分的面积为( )

- A、
- B、 2
- C、 π-1
- D、
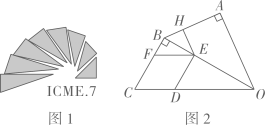
图1是第七届国际数学教育大会(ICME)的会徽,图2由其主体图案中相邻两个直角三角形组合而成.作菱形CDEF,使点D,E,F分别在边OC,OB,BC上,过点 作
作 于点
于点 .当
.当
 时,EH的长为( )
时,EH的长为( )
- A、
- B、
- C、
- D、